La pregunta a contestar es como representamos una superficie a partir de un conjunto de datos con una aproximación de polinomios de Legendre.
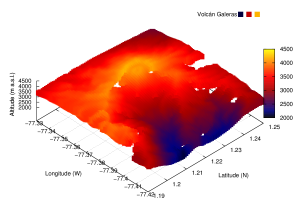
El conjunto de datos analizar corresponde al elrvamiento topográfico en la zona del volcán Galeras, realizado por la NASA durante misiones del Transbordador Espacial mediante radar (instrumento SRTM). Cada punto sobre una cuadrícula de (3×3) segundos de arco (aprox. 90mx90m) y la altitud está en metros sobre el nivel del mar. La imagen muestra las elevaciones topográficas indicada en el código de colores. El borde del volcán y el cráter están claramente visible y la ciudad de Pasto está hacia el Oeste (datos e imagen cortesía de Hernán Asorey)
Las columnas son: #Latitud #Longitud #Altitud
La forma estándar de reconstruir esta superficie es mediante un modelo de regresión de mínimos cuadrados. Otra forma consiste en generar una función a partir de una base de polinomios, típicamente polinomios cúbicos. Hay muchas referencias al respecto. Una clara la pueden encontrar en el libro MACHINE VISION de R. Jain, R. Kasturi, B. G. Schunck McGraw-Hill, 1995 Capt 13 13.7.1 en la cual se aproxima la superficie por un producto tensorial de polinomios cúbicos.
Por otro lado, en un artículo S. Omachi y M. Omachi Fast template matching with polynomials IEEE Transactions on Image Processing, 8 2139–2149 (2007) proponen la reconstrucción de una imagen a partir de una expansión binomial de polinomios de Legendre y justifican que los algoritmos resultantes son más eficientes.
La evaluación consiste que en equipos de trabajo de 2 o 3 personas:0
- Ser capaz de explicar el algoritmo de cómo, a partir de datos experimentales, se genera una superficie mediante una regresión de polinomios cúbicos (2abril).
- Ser capaz de explicar la propuesta de Omachi & Omachi (Sección II del artículo) (2abril)
- Proponer un algoritmo que implemente la propuesta de Omachi & Omachi para reconstruir superficies. En qué se diferencia de la propuesta estándar de BSplines cúbicos (2abril)
- Presentar un plan de trabajo para implementar la propuesta de Omachi & Omachi para reconstruir superficies. (2abril)
- Entregar un reporte escrito (9abril) que incluya
- La reconstrucción de la superficie utilizando cualquier herramienta computacional disponible tipo Pytnon o SciLab, en base a interpolación BSplines de tercer grado. Esto es entregar un archivo con la misma sintaxis pero con una mayor resolución (~10m x 10m)
- Una implementación preliminar de
- Una implementación de la propuesta de Omachi & Omachi para reconstruir superficies